++ 50 ++ (x-y)^3=x^3-y^3-3xy(x-y) 351854-X(x^3-y^3)+3xy(x-y) solution

So we set it = 0 i*sqrt(3)(x1) = 0 x1 = 0 x = 1 Then substituting that y = y = y = y = 1 So we end up with all solutions {(x,y) x y = 1} plus the one solution (x,y) = (1,1) Now if you were asking about xy instead of xy, the answer would be xy is always either 1 or 2 Are you sure you didn't make a typo and you were asking about xy and not xy? = x^3 3x^2y 3xy^2 y^3 = x^3 y^3 3xy(x y) Also, Read Cube of a Binomial Cube of Sum of Two Binomials Examples 1 Determine the expansion of (x 2y)^3 Solution The given expression is (x 2y)^3 We have an equation on cubes like (x y)^3 = x^3 y^3 3xy(x y) By comparing the above expression with the (x y)^3 Here, xWe know that (x y) 3 = x 3 y 3 3xy (x y) Using Identity VII ⇒ x 3 y 3 = (x y) 3 3xy (x y) x 3 y 3 = (x y) { (x y) 2 3xy} ⇒ x 3 y 3 = (x y) (x 2 2xy y 2 3ry) Using Identity IV ⇒ x 3 y 3 = (x y) (x 2 xy y 2 ) 350 Views

Consider The Function F X Y X 3 Y 3 3xy Chegg Com

X(x^3-y^3)+3xy(x-y) solution

X(x^3-y^3)+3xy(x-y) solution-Ĺet x^yy^x= (xy)^3=x^3y^33xy (xy) Or,x^yy^x=x^3y^39xy again x=3y so x^3y^39xy= (3y)^3y^39 (3y)y=2727y9y^2y^3y^39y^227=5427y Now we got 54 27y=27, or 27y=27,y=1 Then x=31=2 The values of x& y only satisfy xy=3 and doen't satisfy x^yy^x=27 So there is no solution for the values of x & y kash EduTech Pvt Ltd What are you looking for?

Find The Asymptotes Of The Following Curves Y 3 3x 2y X Y 2 3x 3 2y 2 2x Y 4x 5y 6 0 Youtube

 If x y = 12, and xy = 27, then find the value of x3 y3 Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queriesĹet x^yy^x=(xy)^3=x^3y^33xy(xy) Or,x^yy^x=x^3y^39xy again x=3y so x^3y^39xy=(3y)^3y^39(3y)y=2727y9y^2y^3y^39y^227=5427y Now we got 54 27y=27, or 27y=27,y=1Polynomial Examples Find the remainder when x 4 x 3 – 2x 2 x 1 is divided by x – 1 Solution Here, p(x) = x 4 x 3 – 2x 2 x

X^3 y^3 = (x y)(x^2 xy y^2) (identity) (2i) = (2i)(x^2 xy y^2) Divide both sides by 2i x^2 xy y^2 = 1 Add 3xy to both sides x^2 2xy y^2 = 3xy 1 (x y)^2 = 3xy 1 (2i)^2 = 3xy 1 4 = 3xy 1 3xy = 3 xy = 1 y = 1/x, xX 0 =1 x a y a = (xy) a, 2 2 3 2 = 6 2;(xy) 3 = x 3 y 3 3xy(x y) x 2 y 2 = (x y)(x y) x2 = 1/x 2, 24 = 1/16 = 1/2 4 (x a)(x b) = x ab;

It is clear that when $x=y$ we have $x^3y^3=0$ Then use long division to divide $x^3y^3$ by $xy$ and the result will be the equation on the right Another way would be to write $$\left(\frac{x}{y}\right)^3 1$$ Now we wish to find the zeros of this polynomialPhilip Macdonald Answered 1 year ago Author has 234 answers and 413K answer views xy =7, xy =1 (xy)^3 = x^3 3x^2*y 3x*y^2 y^3 = x^3y^3 3xy (xy) Then 7^3 = x^3y^3 3*1*7, ie, x^3y^3 = 7^3 7*3 = 7 (7^2 3) = 7*46 =322 143 views Sponsored by Jumbo Privacy & Security (x y z) 2 = x 2 y 2 z 2 2xy 2yz 2zx (x y) 3 = x 3 y 3 3xy(x y) (x – y) 3 = x 3 – y 3 – 3xy(x – y) x 3 y 3 z 3 – 3xyz = (x y z)(x 2 y 2 z 2 – xy – yz – zx;

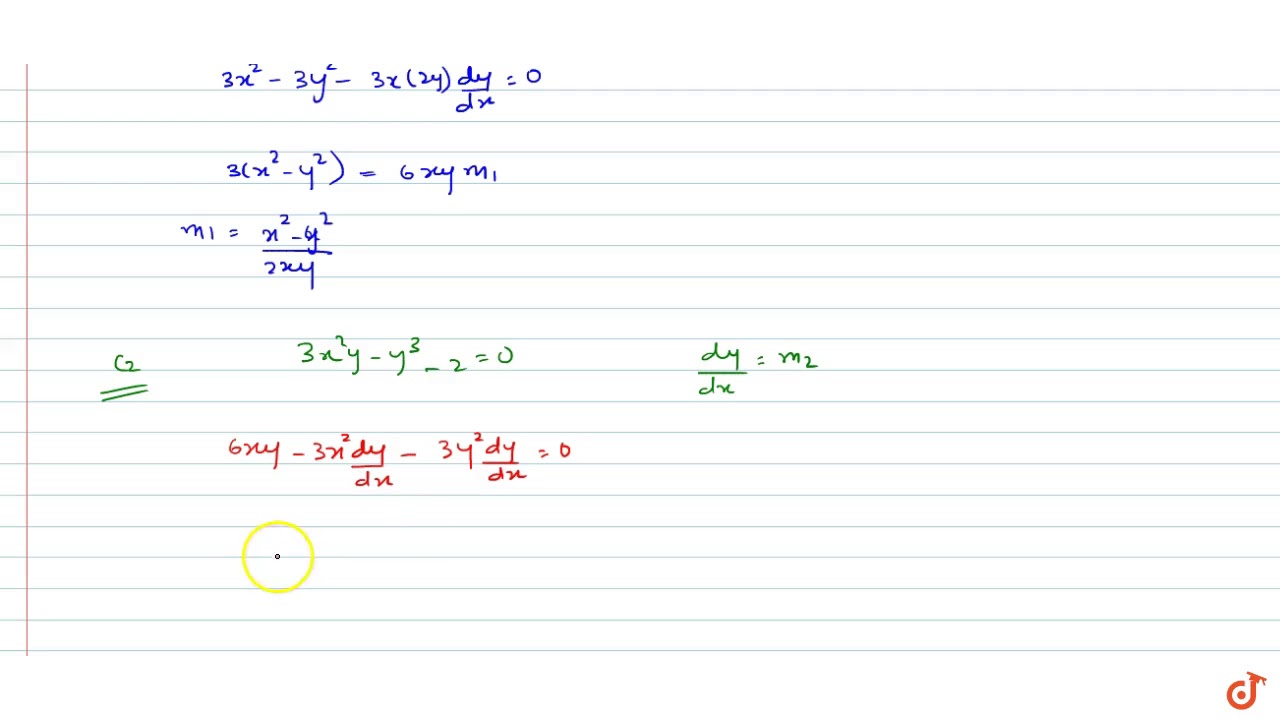
The Two Curves X 3 3xy 2 2 0 And 3x 2y Y 3 2 0 Youtube

Find The Asymptotes Of The Following Curves Y 3 3x 2y X Y 2 3x 3 2y 2 2x Y 4x 5y 6 0 Youtube

Solution (By Examveda Team) Given, xy = 2 cubing both sides (xy) 3 = 2 3 => x 3 y 3 3xy ( xy) = 8 => x 3 y 3 3×15×2= 8 => x 3 y 3 90 = 8 => x 3 y 3 = 035 (1) Upvote (1) Choose An Option That Best Describes Your Problem Answer not in Detail Incomplete Answer Answer Incorrect Others Answer not in Detail Incomplete Answer Answer IncorrectCube of a binomial can be simplified using the identities \({(x y)}^3 = x^3 y^3 3xy(x y)\)

X Y 3 X 3 Y 3 3xy X Y Verify Maths Meritnation Com

If X 3 3xy 2 14 Y 3 3yx 2 13 And X Y Are Real Find The Maths Polynomials Meritnation Com

 4 It's two equations, with two variables We can do what we always do You can write y = 8 / x, and substitute into the first equation, obtaining x3 / x3 = 72 From here, we want to write this as a polynomial, so we multiply through x3 so there are no negative powers, and then move everything to the left(xy)^3 x^3y^33xy(xy) x^3y^3z^33xyz (xyz)(x^2y^2z^2xyyzzx) √ab √a√b √a/b(whole) √a/√b (√a√b)(√a√b) ab (a√b)(a√b) a^2b (√a√b)^2 a2√abb OTHER SETS BY THIS CREATOR GeographyChapter 1Indiasize and location 13 terms ikeepchangingmynameStudy on the go Download the iOS Download the Android app Company About Us Scholarships

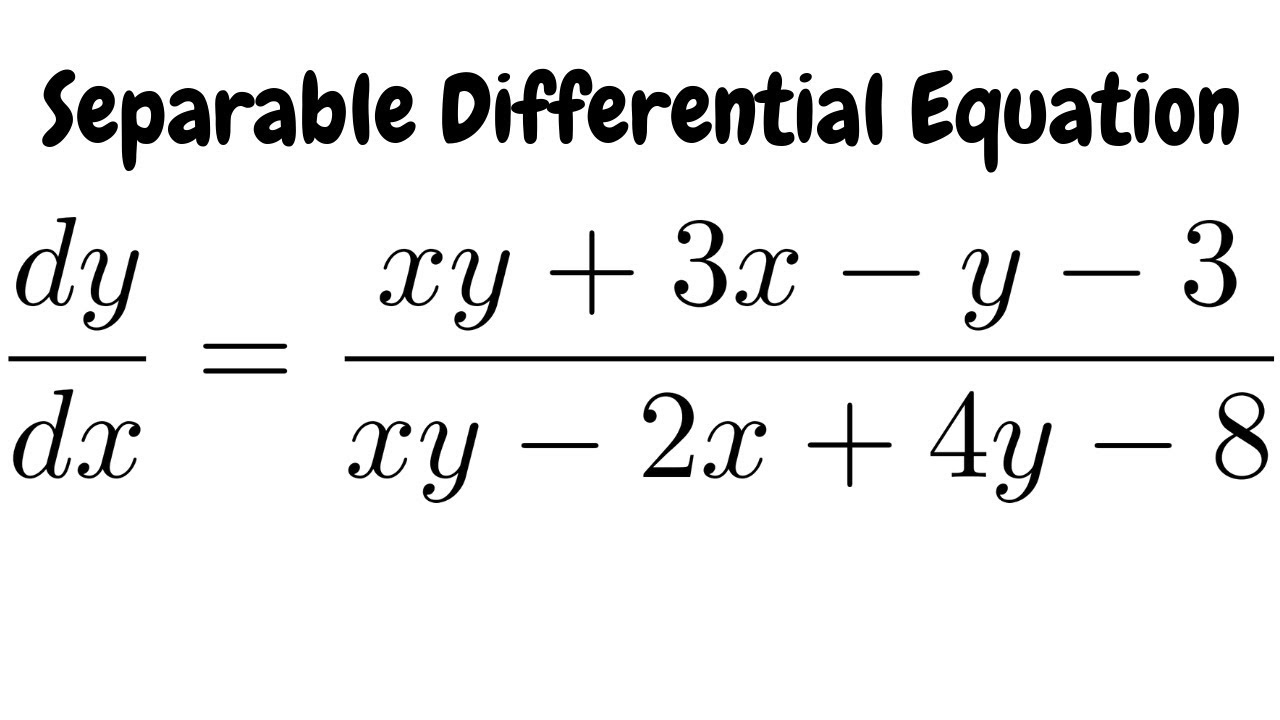
Separable Differential Equation Dy Dx Xy 3x Y 3 Xy 2x 4y 8 Youtube

1

 kdtiwari9862 is waiting for your help Add your answer and earn points ashwinipmashwinipm Answer 3xyz Stepbystep explanation x y z = 0 = x y = z Cubing on both sides (x y)^3 = (z)^3 ⇒x ^3y ^33xy(xy)=z ^3Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyX 3 y 3 3xy = 1

Factories X3 9y3 3xy X Y Brainly In

Let F X Y X 3 3xy 2 2y 3 Show That The Chegg Com

 Here, exponent of every variable is a whole number, but x 10 y 3 t 50 is a polynomial in x, y and t, ie, in three variables So, it is not a polynomial in one variable Ex 21 Class 9 Maths Question 2 (ii) (2a – 3b) 3 = (2a) 3 – (3b) 33(2a)(3b)(2a3b) Using identity (xy) 3 =x 3y 33xy(xy) = 8a 327b 318ab(2a3b) = 8a 3 – 27 b 3 – 36a 2 b 54ab 2 =8a 3 – 36a 2 b 54ab 2 – 27 b 3 Question 7 Evaluate the following using suitable identities (i) (99) 3Quadratic equation, for any given x if ax 2 bx c =0 then x has 2 solutions x=(b√(b 2 4ac)/2a, x=(b√(b 2 4ac)/2a x a y b is not equal to (xy) ab

If X 3 Y 3 1 3xy Where X Y Determine The Value Of X Y 1

Consider The Function F X Y X 3 Y 3 3xy Chegg Com

 0 Follow 0 A K Daya Sir, added an answer, on 25/9/13 A K Daya Sir answered this x 3 y 3 = (x y) (x 2 xy y 2 ) this formula can be derived from (x y) 3 = x 3 y 3 3xy (x y) x 3 y 3 = (x y) 3 3xy (x y) x 3 y 3 = (x y) (x y) 2 3xy = (x y) x 2 y 2 2xy 3xy = (x y) (x 2 xy y 2 ) Was this answer helpful?Simplify (xy)^3 (x − y)3 ( x y) 3 Use the Binomial Theorem x3 3x2(−y) 3x(−y)2 (−y)3 x 3 3 x 2 ( y) 3 x ( y) 2 ( y) 3 Simplify each term Tap for more steps Rewrite using the commutative property of multiplication x 3 3 ⋅ − 1 ( x 2 y) 3 x ( − y) 2 ( − y) 3 x 3 3 ⋅ 1 ( x 2 y) 3 x ( y) 2 find x^3y^3 The coordinates of point Y are giving The midpoint XY is (3,5) Find the coordinates of point X

Relplot Equation Plotter

If X 3 Y 3 9 And X Y 3 Then What Is The Value Of X 4 Y 4 Quora

Typo/misspeak around 4 minutes 369=27Multivariable Calculus Find all local maxima/minima and saddle points for the function f(x,y) = x^3 3xy y^3 WHere given are, XY=7, let's say it is formula 1 in order to make it kinda convenient and easy to understand And XY=10, let's mark it as 2 Now, see formula 1 can be also written as,1 How do you simplify the cube of a binomial?

X 3 3x 2 X 3 Factorise Novocom Top

How To Know At A Glance That Math X 3 3xy 2 2y 3 Math Is Factorable Quora

 Which of the following is a factor of `(xy)^3(x^3y^3)?` A `x^2y^22xy` B `x^2y^2xy` C `xy^2` D `3xy` Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queriesSOLUTION ⇒ x – y = 3 ⇒ (x – y) 3 = 3 3 ⇒ x 3 – y 3 – 3xy (x – y) = 27 ⇒ x 3 – y 3 – 3xy × 3 = 27 ⇒ x 3 – y 3 – 9xy = 27(i) (99) 3 (ii) (102) 3 (iii) (998) 3 Solution We will use the following algebraic Identities to evaluate the given expressions (x y) 3 = x 3 y 3 3xy(x y) (x y) 3 = x 3 y 3 3xy(x y) (i) (99) 3 = (100 1) 3 Identity Here we can use (x y) 3 = x 3 y 3 3xy(x y) Let us substitute x = 100, y = 1 (99) 3 = (100) 3 (1) 3 3(100)(1)(100 1)

Find All Values Of X Y Where Theorem 3 1 1 The Chegg Com

If X 3 3xy 2y 3 17 Then In Terms Of X And Y Chegg Com

 Give possible expressions for the length and breadth of each of the following rectangles, in which their areas are given (i) Area 25a2 – 35a 12 (ii) Area 35y2 13y – 12 Solution (i) We have, area of rectangle = 25a 2 – 35a12 = 25a 2 – a – 15a12 Thanks for trying but the answer is 459 dududsu2 #3 1 x= 9y xy would then be (9y) y = 10 y^2 9y 10 = 0 y^29y10 = 0 y = 9/2 sqrt41/ 2 (x^3 y^3 = ( Start your 48hour free trial to unlock this answer and thousands more Enjoy eNotes adfree and cancel anytime

X 3 3x 2 X 3 Factorise Novocom Top

Analyze The Product Of X 3 9y 3 3xy X Y

Get FREE NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 25 We have created Step by Step solutions for Class 9 maths to help you to revise(x y)^3 = (x^3) (y^3) 3xy(x y) so, (3)^3 = 9 3xy(3) so, 27 = 9 9xy so, (27 9)/9 = xy so, xy = 18/9 = 2X a /x b = x ab = 1/x ba;

1

If X 3 Y 3 3xy 2 3x 2y 1 0 Then At 0 1 Dy Dx Youtube

 = (4a – 3b) 3 ∵ (x – y) 3 = x 3 – y 3 – 3xy(x – y) = (40 – 3b) (4a – 3b) (4a – 3b) Question 3 What are the possible expressions for the dimensions of a cuboid whose volume is given below ?यदि x 2 – 9x 1 = 0 है, तो x 3 1/x 3 का मान क्या है?In mathematics, the cube of sum of two terms is expressed as the cube of binomial x y It is read as x plus y whole cube It is mainly used in mathematics as a formula for expanding cube of sum of any two terms in their terms ( x y) 3 = x 3 y 3 3 x 2 y 3 x y 2

Solve X 3 3xy 2 Dx Y 3 3x 2y Dy Sarthaks Econnect Largest Online Education Community

Factorise X X3 Y3 3xy X Y Brainly In

Volume = 12ky 2 8ky – k Solution We have, volume = 12ky 2 8ky – k = 4k(3y 2 2y – 5) = 4k(3y 2 5y – 3y – 5)(X – Y) 3 = X 3 – Y 3 – 3XY(X – Y) Or (X – Y) 3 = X 3 – Y 3 – 3X 2 Y 3XY 2 Was this answer helpful?Ĺet x^yy^x=(xy)^3=x^3y^33xy(xy) Or,x^yy^x=x^3y^39xy again x=3y so x^3y^39xy=(3y)^3y^39(3y)y=2727y9y^2y^3y^39y^227=5427y Now we got 54 27y=27, or 27y=27,y=1

Factorise X Y 3 X 3 Y 3 3xy X Y Brainly In

Let F X Y X 3 3x 2y 3 2y 2 We Find Fx X Y 3x 2 Chegg Com

 Heya mate, Here is ur answer xyz=0 xy=z cubing both the sides (xy)^3=z^3 x^3 y^3 3xy (xy) =z^3 but xy=z x^3 y^3 3xy (z) =z^3 x^3 Y^3 3xyz=z^31 Explanation We know that algebraic formula, (x y) 3 = x 3 y 3 3xy (x y) put the value of x y in given equation given, x y = 1 1 = x 3 y 3 3xy X 1?Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more

How To Factorise Using The Identity X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Youtube

Cho X Y 1 Tinh Gia Trị Của Biểu Thức X 3 Y 3 3xy Cho X Y 1 Tinh Gia Trị Của Biểu Thức X 3 Y 3

 xy=1 (xy)³=1 x³3x²y3xy²y³=1 3xy(xy)3=1 xy=2/3 (xy)²=1 x²y²2xy=1 x²y²=7/3 (x²y²)(x³y³)=7/3*3=7 x^5x²y³x³y²y^5=7 x^5y^5=x²y²(xy)7=4/97=59/9 已赞Telangana SCERT Class 9 Math Chapter 2 Polynomials and Factorisation Exercise 25 Math Problems and Solution Here in this Post Telanagana SCERT Class 9 Math Solution Chapter 2 Polynomials and Factorisation Exercise 25Use identity ( a b)^3 = a^3 b^3 3ab (a b ) Put a= x and b= y ( x y)^3 = x^3 y^3 3xy ( x y ) In further step 3xy can be multiplied inside the bracket The answer is 👍 Helpful 💡

Locus Of All Point P X Y Satisfying X 3 Y 3 3xy 1 Consists Of Union Of Sarthaks Econnect Largest Online Education Community

X X3 Y3 3xy X Y Brainly In

Note that (x y) 3 = x 3 y 3 3xy(x y) Share this link with a friend Copied! 展开全部 (xy)^3= (xy)^2* (xy)= (x^22xyy^2)* (xy)=x^3y^33xy (xy) 所以得到上述证明 这是一个简单的证明，你应该还没有接触到 (xy)^3 4 已赞过 已踩过 < 你对这个回答的评价是？ 分享 新浪微博 Q9 Verify (i) x 3 y 3 = (x y) (x 2 – xy y 2) (ii) x 3 – y 3 = (x – y) (x 2 xy y 2) Answer (i) x 3 y 3 = (x y) (x 2 – xy y 2) ∵ (x y) 3

Www Ma Utexas Edu Users Rav M408d F10 M408d Quiz6 Solutions Pdf

Ppt Polynomials Powerpoint Presentation Free Download Id

SOLUTION ⇒ x – y = 3 ⇒ (x – y) 3 = 3 3 ⇒ x 3 – y 3 – 3xy (x – y) = 27 ⇒ x 3 – y 3 – 3xy × 3 = 27 ⇒ x 3 – y 3 – 9xy = 27 Related Questions If x 2 – 9x 1 = 0, then what is the value of x 3 1/x 3?

X Y 3 X3 Y3 3xy X Y Proof It Maths Polynomials Meritnation Com

Simplify The Expression X 3 Y 3 X Y 2 3xy X Y 2 3xy X 3 Y 3 X Xy X 2 Y 2 Sarthaks Econnect Largest Online Education Community

X X3 Y3 3xy X Y Maths Polynomials Meritnation Com

Solve Dy Dx 3xy Xy 3 30 Dy Dx X 2y 3 2x Chegg Com

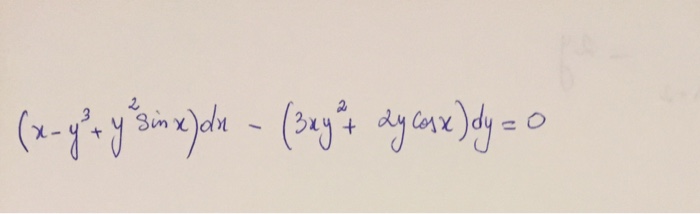
X Y 3 Y 2 Sin X Dx 3xy 2 2y Cosx Dy 0 Chegg Com

What Is The Solution To This Homogeneous Differential Equation Dy Dx Y 3 3x 2y X 3 3xy 2 Quora

Given That X Y In R Solve 4x 2 3xy 2xy 3x 2 Iota 4y 2 X 2 2 3xy 2y 2 Iota Youtube

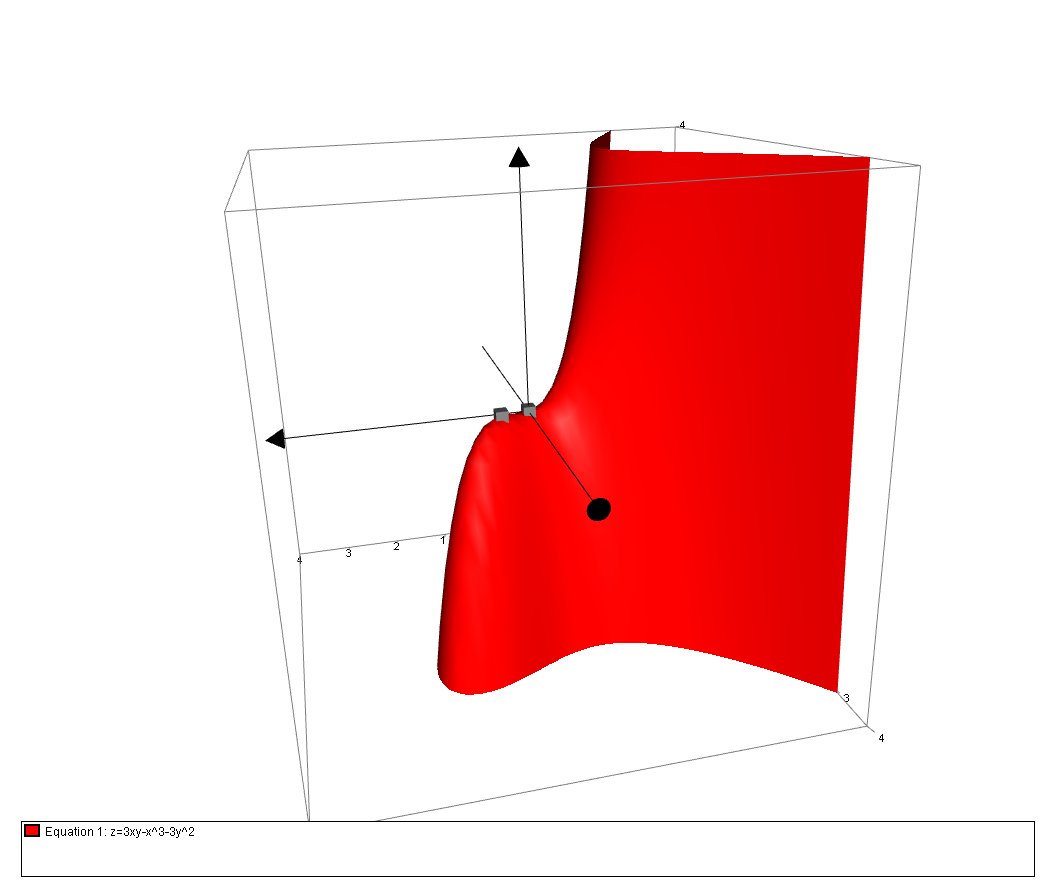
Identify The Critical Points For The Function F X Y 3xy X 3 3y 2 Socratic

If X 3 Y 2 3xy X Y Then Log X Y 3

Search Q X Y 5e3 Expand Formula Tbm Isch

Factorise X3 9y3 3xy X Y Brainly In

Find The Extreme Values Of The Function X 3 Y 3 3xy Sarthaks Econnect Largest Online Education Community

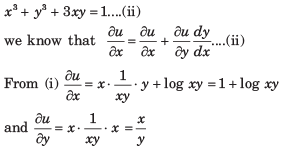
If U X Log Xy Wherex3 Y3 3xy 1 Then Du Dx Is Equal Toa B C D Correct Answer Is Option A Can You Explain This Answer Edurev Electronics And Communication Engineering Ece

Verify X Y 3 X3 Y3 3xy X Y Brainly In

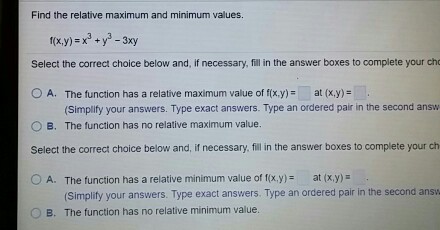
Find The Relative Maximum And Minimum Values F X Chegg Com

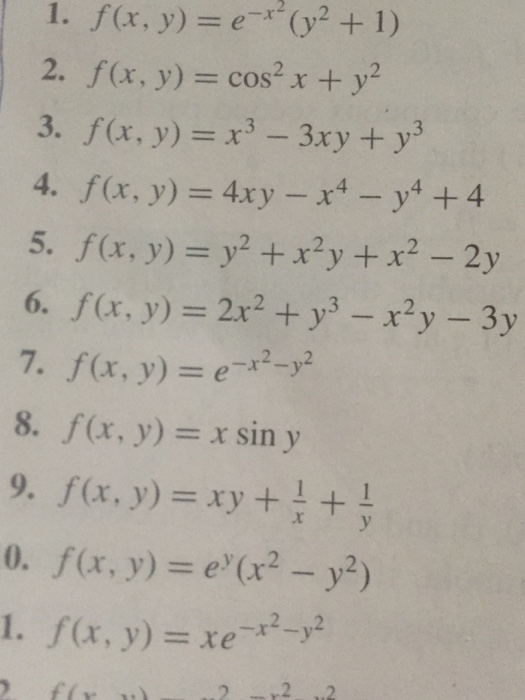
F X Y E X 2 Y 2 1 F X Y Cos 2 X Y 2 Chegg Com

X Y 3 X3 Y3 3xy X Y Brainly In

X 3 Y 3 Z 3 Novocom Top

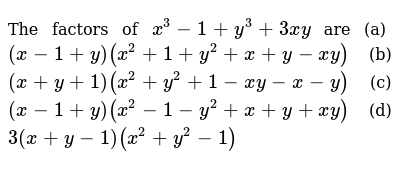
Rewrite The Slope Intercept Equation Of The Line Y 1 3 X 2 In

If X Y 2 Then What Is The Value Of X Y 6xy Quora

X 3 3xy 2 Dx Y 3 3x 2y Dy Youtube

How To Evaluate Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube

If X Y 7 And X3 Y3 133 Find I Xyii X Y Brainly In

Expand X X Y 3 3xy X Y

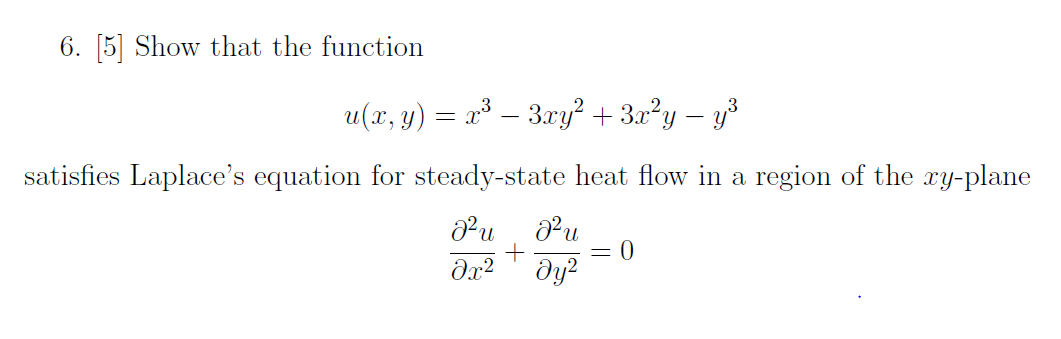
Show That The Function U X Y X 3 3xy 2 3x 2y Chegg Com

Factorise X3 9y3 3xy X Y Brainly In

If Math X 3 Y 3 3xy 1 Math What Is The Minimum Value Of Math X 2 Y 2 Math Quora

If A X 3 Y 3 X Y 2 3xy B X Y 2 3xy X 3 Y 3 C Xy

X Y 3 X3 Y3 3xy X Y Proof It Maths Polynomials Meritnation Com

Maximum Value Of The Function F X Y X 3 Y 3 3xy Is Sarthaks Econnect Largest Online Education Community

Prove That X2 Y2 C X2 Y2 2 Is The General Solution Of The Differential Equation X3 3xy2 Dx Y3 3x2y Dy Where C Is Parameter Mathematics Shaalaa Com

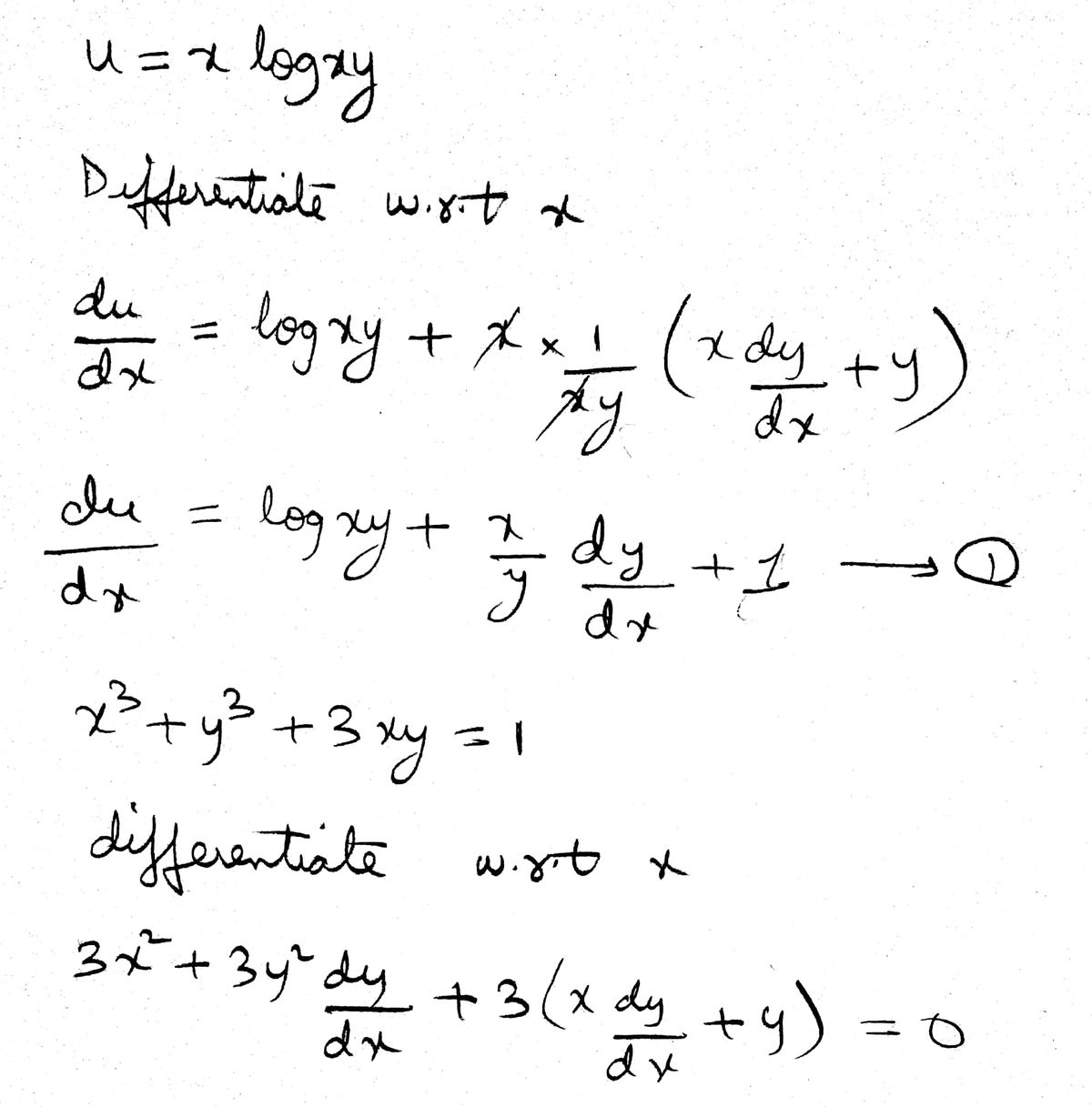
Answered If U X Log Xy Where X3 Y3 3xy 1 Find Bartleby

X X 3 Y 3 3xy X Y

X Y 3 X3 Y3 3xy X Y Brainly In

If A Line Y 3 X Cuts The Curve X 3 Y 3 3xy 5x 2 3y 2 4x 5y 1 0 At The Points A B And C

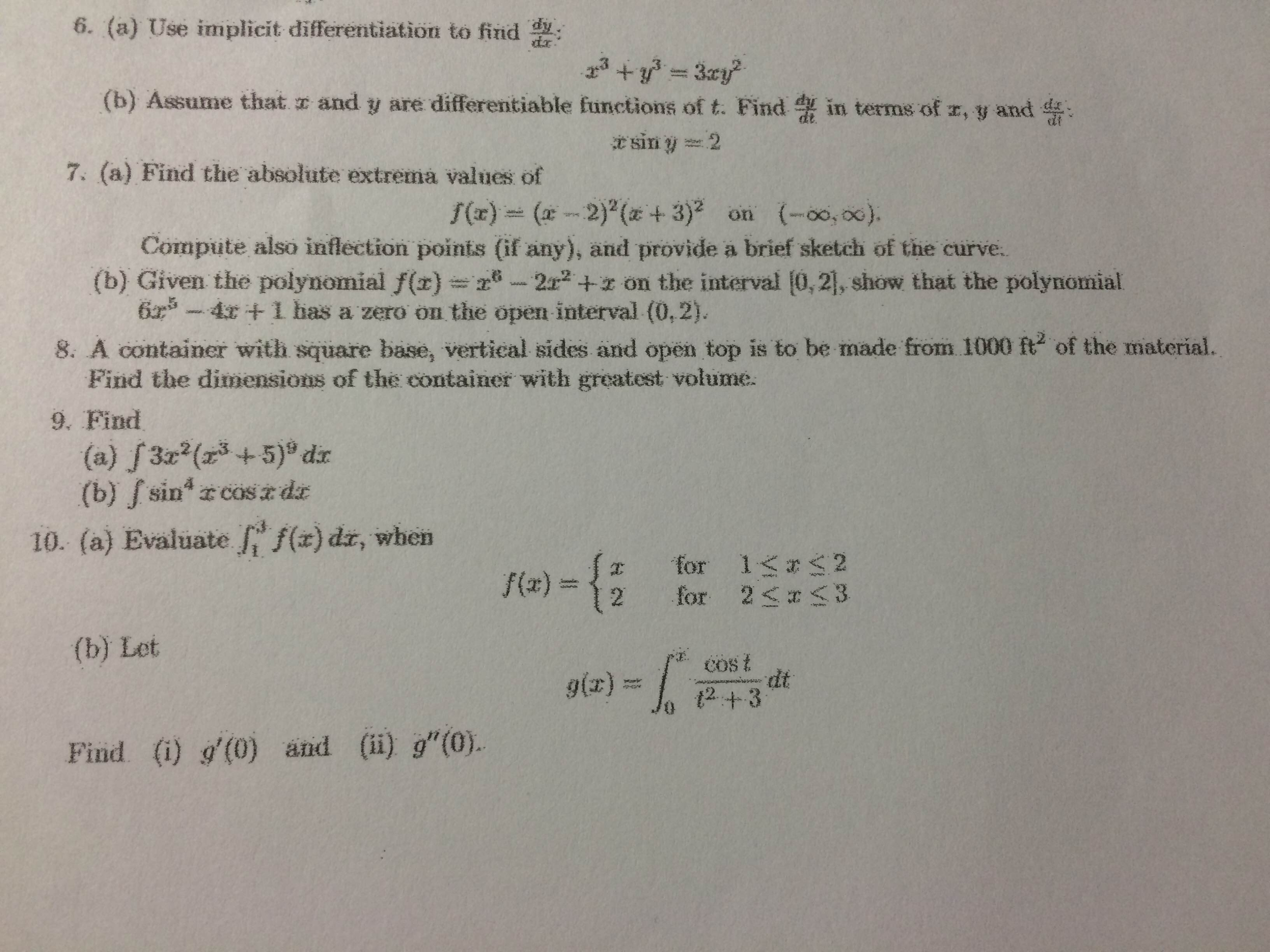
6 A Use Implicit Differentiation To Find Dy Dx Chegg Com

How To Draw The Graph Of X 3 Y 3 3xy Quora

What Are The Factors Of X Y 3 X3 Y3 Brainly In

Find The Critical Points Of F X Y 4 X 3 Y 3 Chegg Com

Find The Local Extrema Of F X Y X 3 3xy Y 3 Chegg Com

3 A Classify Each Ode By Order And Linearity Y 3xy Xy 0 Homeworklib

How To Solve Math Xy 2 Dy X 3 Y 3 Dx 0 Math Quora

Find The Critical Points Of F X Y X 3 Y 3 3xy Chegg Com

Solve Differential Equation X 3 3xy 2 Dx Y 3 3x 2y Dy Maths Differential Equations Meritnation Com

K 6y Y 1 7y 7y Jndei M 3x 4x N 6x X Je Gauthmath

How To Solve The General Solution Of X 3 Y 3 Dx Xy 2dy 0 Quora

If Math 3x 4y Sqrt Xy Math How Can You Prove That Math X 2 Y 2 Xy Math Quora

X X3 Y3 3xy X Y Maths Polynomials Meritnation Com

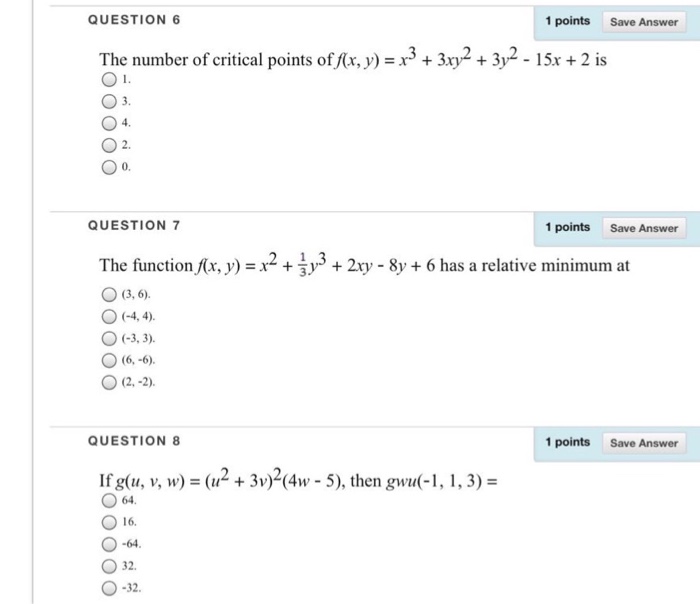
The Number Of Critical Points Of F X Y X 3 Chegg Com

If X Y 1 Then Find The Value Of X 3 Y 3 3xy Maths Continuity And Differentiability Meritnation Com

Find Dydx Where X 3 Y 3 3xy 7

If X Y 7 And X 3 Y 3 133 Find X 2 Y 2 Brainly In

X3 9y3 3xy X Y এর উৎপ দক ব শ ল ষণ কর Brainly In

How To Verify Algebric Identity X Y 3 X3 3xy X Y Y3 Maths Polynomials Meritnation Com

न म न व य जक क ग णनखण ड क ज य X X 3 Y 3 3xy X Y Youtube

If X Y 12 And Xy 27 Then Find The Value Of X3 Y3 Polynomials Maths Class 9

Ppt Polynomials Powerpoint Presentation Free Download Id

How To Solve Math X 3 Y 3 Dx 3xy 2dy 0 Quora

Y3 3xy2 X3 3x2y Find Dy Dx Plzzzzzzzzzzz Slove Ths As Fast As Possible Maths Continuity And Differentiability Meritnation Com

1

Proof Of Formulae I X Y 3 X 3 Y 3 3xy X Y Ii X 3

Find Dy Dx By Implicit Differentiation X 2 Y 2 Chegg Com

If X 3 Y 3 9 And X Y 3 Then The Value Of X 4 Y 4 Please Answer Honestly Don T Watch Others Quora

How To Solve X 3 3xy 2 Dx 3x 2y Y 3 Dy Quora

Factorize X X 3 Y 3 3xy X Y Sarthaks Econnect Largest Online Education Community

How To Evaluate Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube

How To Factorise Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube

Second Partials Test For F X Y X 3 3xy Y 3 Youtube

Transform X 3 Y 3 3xy 0 Mathematics Stack Exchange

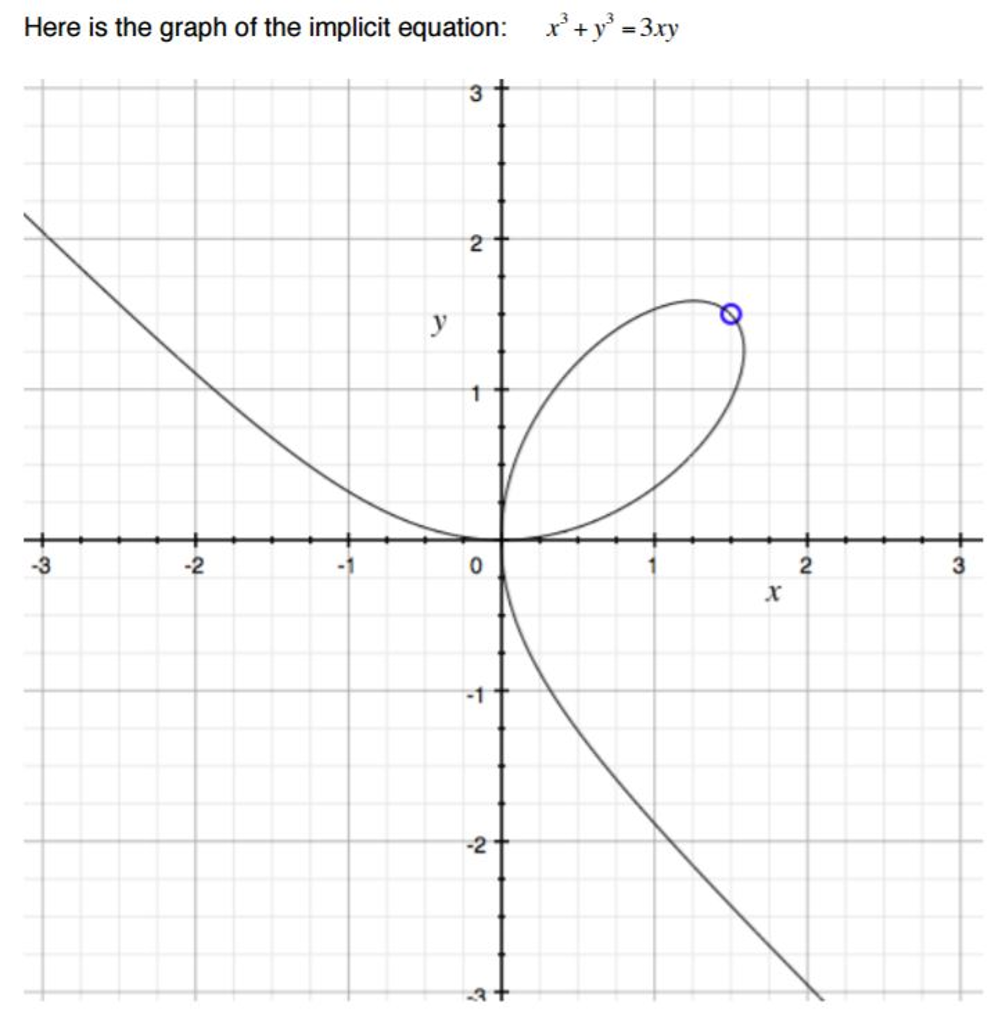
Here Is The Graph Of The Implicit Equation X 3 Y 3 Chegg Com

X 3 Y 3 3xy 2 Find Dy Dx Using Implicit Differentiation Youtube

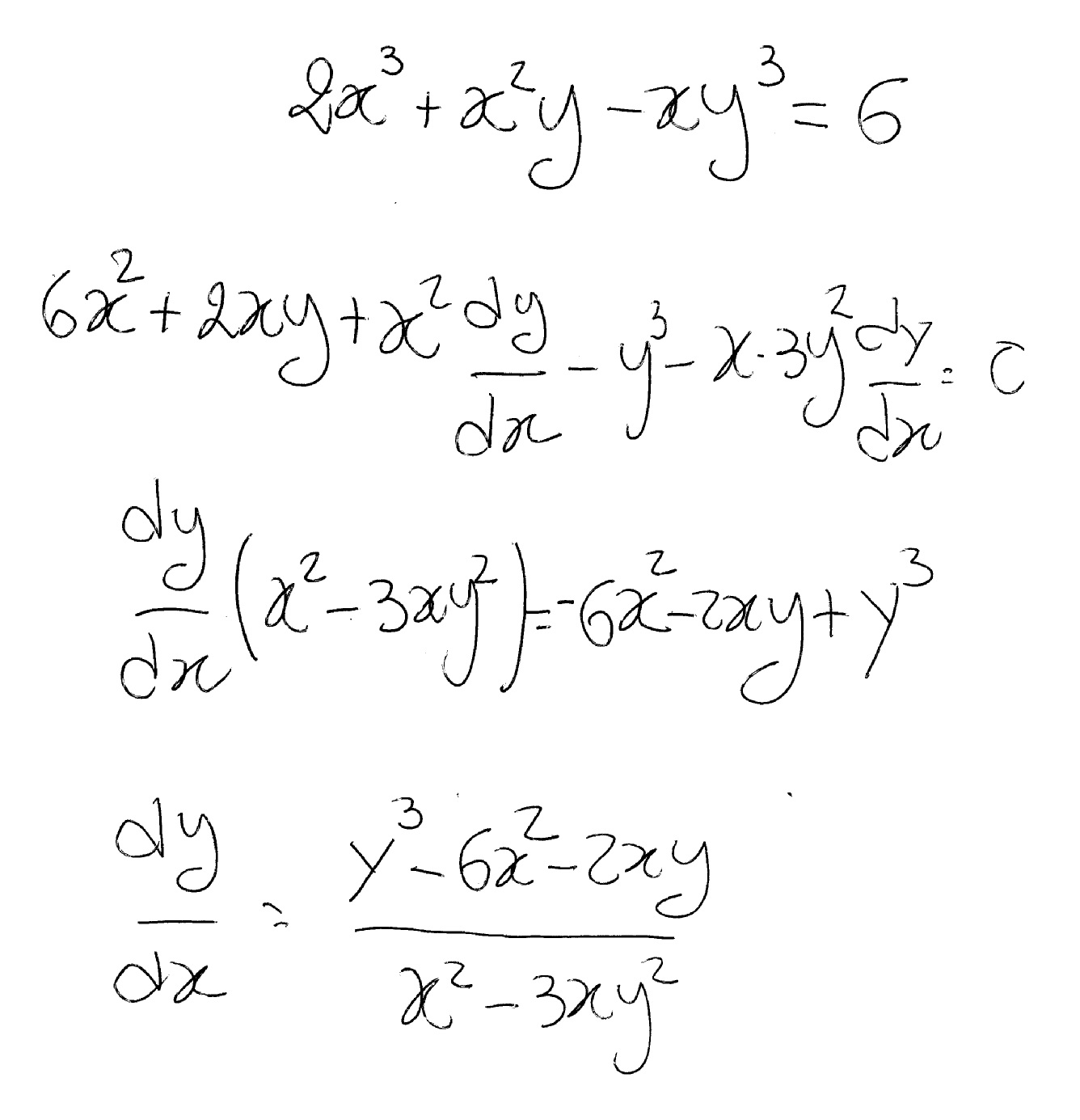
How Do You Find Dy Dx By Implicit Differentiation For 2x 3 X 2 Y Xy 3 6 Socratic

Factorise X3 9y3 3xy X Y Brainly In

Verify X3 Y3 And X3 Y3 Std 9 Maths Ex 2 5 Q 9 Youtube

Incoming Term: (x+y)^3=x^3+y^3+3xy(x+y), x(x^3-y^3)+3xy(x-y) solution, x^3+y^3+z^3=(x+y)^3-3xy(x+y)+z^3, (x+y)3=x3+y3+3xy(x+y),